Sometimes, 64 bits of resolution just isn’t enough — especially when floating point arithmetic only uses 53 of those bits for the significand. There are arbitrary-precision libraries out there, but it would be nice to have larger floating-point formats supported by the compiler.
It turns out that the floating-point units on x86 processors (32- and 64-bit) support an 80-bit “extended precision” type — and GCC/mingw supports this as type “long double.”
It’s not quite the 128 bits of floating-point goodness you’d expect based on sizeof(long double) — each such variable takes 128 bits — sixteen bytes — of space! Along with this extended precision, printf() now (once you know how to ask nicely) also will print digits to 62 points past the decimal place before switching to zeros. (Exactly how many of these digits mean anything is debatable, but at least it won’t introduce an artificial precision limitation.)
Using printf() and friends on long doubles works well: the format string is %Lf. In order for mingw to understand this format string, though, you’ll need to include the following line:
#define __USE_MINGW_ANSI_STDIO 1
I decided to see how the extra precision worked by computing pi. The algorithm I chose is numeric integration by the trapezoid method of 1/4 of the unit circle (and then multiplying by 4.) If your sums are precise enough, you should get roughly as many digits of Pi as the log10 of the number of samples.
I wrote the following program to compare the precision performance of <float> vs. <double> vs. <long double>. 32-bit floats stopped getting more accurate at 2^18 slices, and froze altogether at 2^25 slices (I suspect dx became indistinguishable from zero.) 64-bit double precision did better, overshooting a little at 2^38 slices. Long double is still going strong at 2^42 and might get another two digits (90 –> 89) on the next iteration. Maybe.
Printing the calculated digits of Pi at each resolution shows the differences:
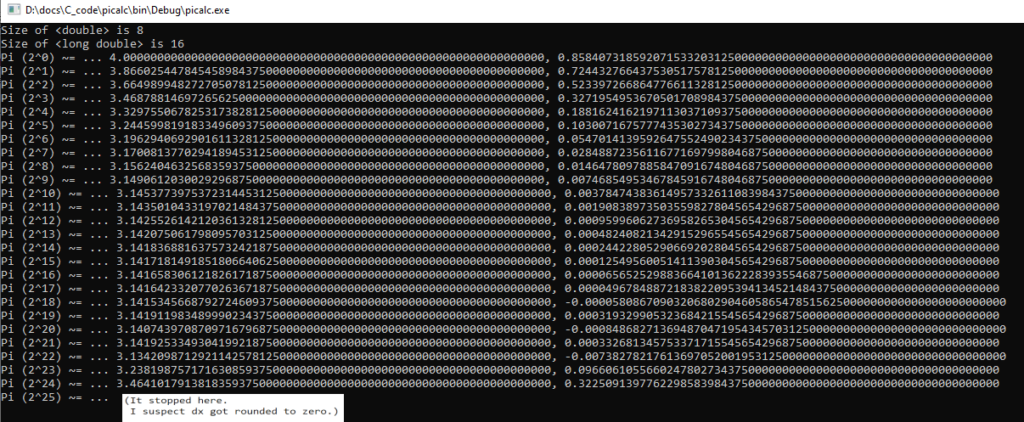
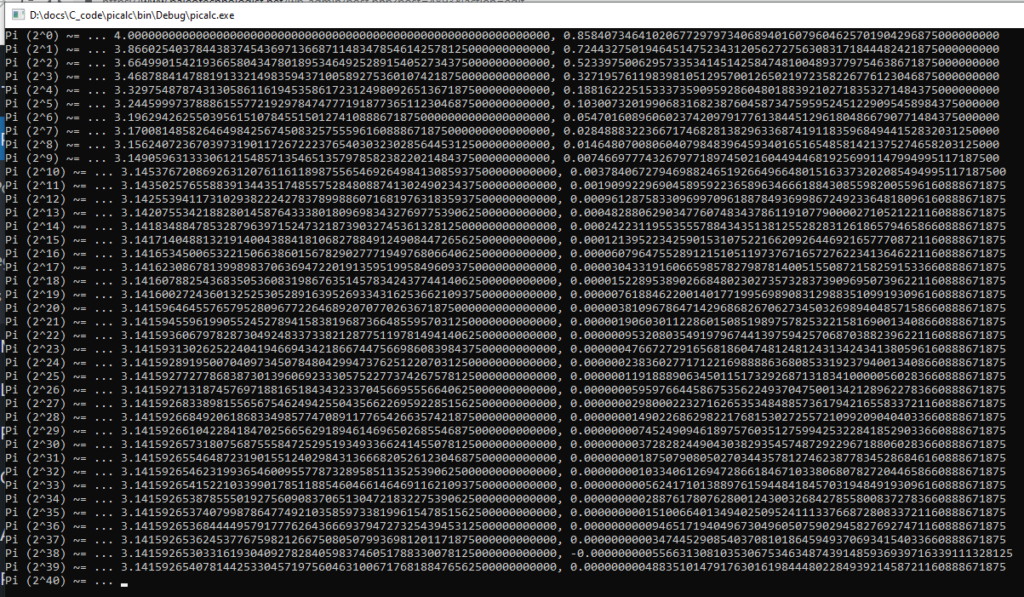
(It overshot on 2^39, which should not happen, and may be stuck on 2^40…)
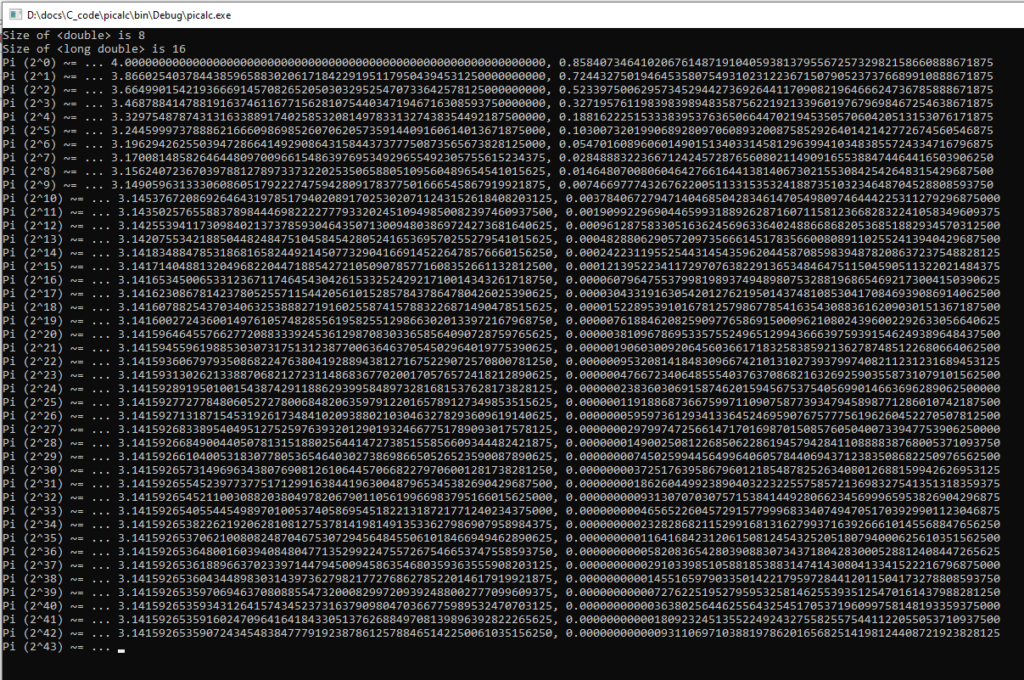
Comparing the latest result from <double> and <long double> — 2^39 — we get:
Float: 3.1416 (best result at 2^17; it then overshot and eventually hung)
64-bit Double: 3.1415926540781… (8 digits past the point)
Long Double: 3.14159265359706… (10.5 digits; even the 9 is correct with rounding.)
Another question (which I’m not tracking this time) is how long each of these take, on the desktop computer as well as on the Samsung A71. The desktop may well be a lot faster at floating point — as an informal comparison, both the desktop and A71 were running overnight; the PC got to ~2^42 and the A71 got to ~2^36, both having started roughly at the same time and run for roughly ten hours. Each level takes as long as all previous levels, so a gap of six levels completed is a 2^6, or 64x, gap in performance.
Maybe it’s not time to retire the desktops for big-data calculations, after all.

