Evolution by natural selection is a powerful algorithm that has come up with all of the variety of life we see on Earth. By keeping what works and discarding the ideas that don’t, populations can evolve over time to better fit their environment.
The same idea can be used to find solutions to given computational problems, as well. The field of Genetic Algorithms / Genetic Programming uses Darwinian evolution to search for solutions to various problems. Candidate solutions are encoded as gene sequences — perhaps a series of bytes, with each byte representing some parameter of the candidate solution. Each generation, the solutions are all tested and ranked, with better solutions having a higher chance to be selected to produce the next generation. Selected parent genomes are combined via crossover (with some mutation) to produce new genomes to be evaluated in the next generation.
One good way to test how well such an approach works is to try it out on problems for which you already know at least some solutions. For example, the Tammes Problem asks what is the greatest size disc for which you can fit N such discs on the surface of a sphere. Equivalently, what is the maximum, minimum distance possible between any two of N points on the surface of a sphere?
Solutions to such a problem can be expressed in genetic form, suitable for being acted upon by evolutionary forces. The position of each point is expressed in altitude and azimuth angles, sufficient to cover the surface of the unit sphere. (Note to self: explore using quaternions.) The simulation is then run, with the function that determines evolutionary fitness being the minimum distance between any two points. Solutions can then be visualized as polyhedra, where the unit sphere is cut by planes normal to the vector from the origin to each point. This results in an N-sided polyhedron — although sometimes a rather weird, lumpy one at first.
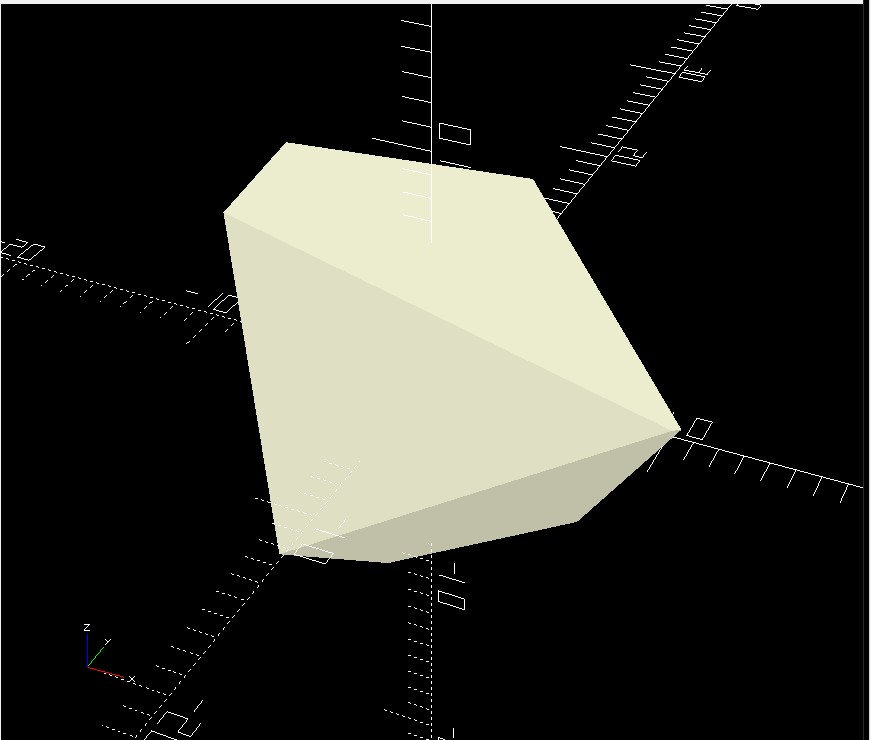
Not very impressive at some 19.3% error — but that quickly improves!
For “easy” problems such as N=6, this approach quickly produces a nearly-optimal solution. Six equally-spaced points on the unit sphere will be farthest apart when they are in the form of a cube. For example, points at (1,0,0) and (0,1,0) could be two such points, 90 degrees apart. The optimal Tammes distance for N=6, then, is sqrt(2).
For N=6, the genetic approach described above very quickly converges to the expected cube solution, with point positions very nearly the expected distance apart. (A typical result differs from sqrt(2) by well under one part per million, if left to run for a while.)
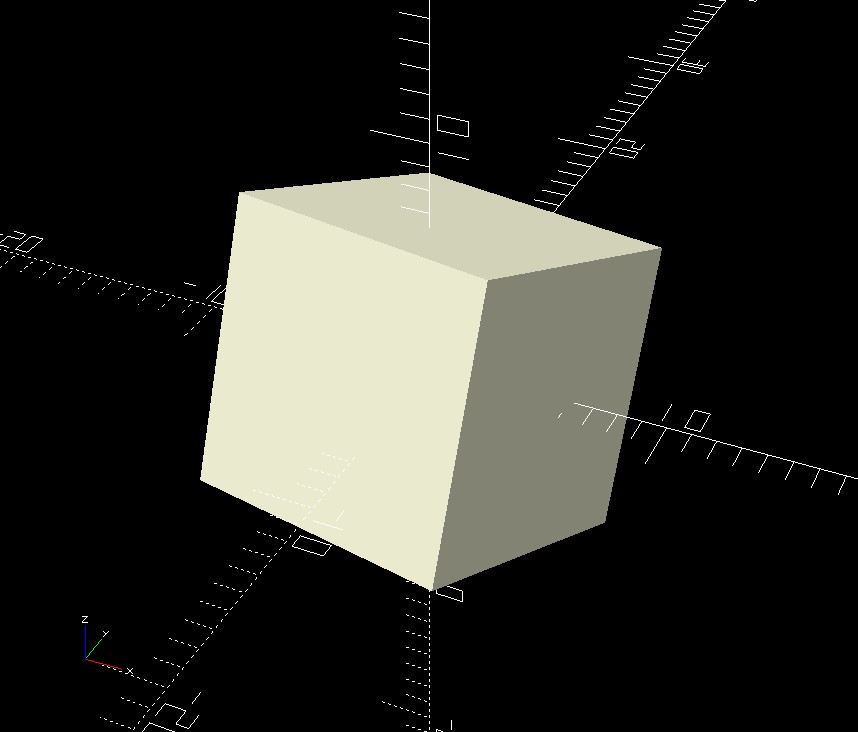
a cube with a measurement error of ~12.293 parts per million.)
Some values of N produce interesting results. For N=8, the most typical result is an anti-prism, similar to the platonic octohedron, but with four of the points rotated by 45 degrees. (When you think about it, it makes sense; the points are farther apart that way.)

Larger values seem to pose greater challenges to this approach; N=12 sometimes produces the expected Platonic regular dodecahedron, but more often will get stuck in a local minimum, producing a somewhat symmetrical shape. (Like in nature, Darwinian evolution doesn’t always produce a *perfect* solution — just whatever seems to get the job done best. )

All except for the 8-gon are irregular, but with striking symmetries.
From left to right: Irregular 10-sider; antiprism 8-sider; 7-hedron; 9-hedron.
The next goal: try to grow a regular icosahedron.