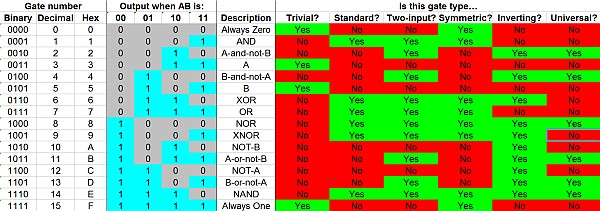
By now, there is no doubt that we’re in the “Digital Age.” Everywhere you look, computers and other digital electronic devices are doing everything from carrying our telephone conversations to controlling our car engines to running our electronic toothbrushes.
Is this “digital” thing just another fad? Is this whole “Digital Revolution” just a way for manufacturers to sell us “upgraded” products, when the old ones would have worked just as well? What is “digital” anyway — and what benefits do we get from switching to “digital” technology?
There are plenty of important benefits — and it’s absolutely not an understatement to call digital technology a “revolution.” To understand why, it’s important to first understand the fundamental difference between “digital” technology and “analog” technology. Here is a brief explanation of what “digital” is, why it’s important, and (at a high level) how it makes the magic of the modern world possible. Sound recording is a good place to start.
In analog technology, signals (voltages or currents, in electronics) are continuously variable. An analog signal, for example, could range between zero and ten volts — or could take on any value in between. Zero volts is OK; ten volts is OK; so is 3.34523607 volts. None of these values necessarily have any special meaning in analog electronics — they generally correspond to, say, the audio waveform to be sent to a speaker. The sounds of a Beach Boys concert are picked up by a microphone and those “good vibrations” are transmitted, amplified but otherwise more or less unchanged, to a tape recorder.
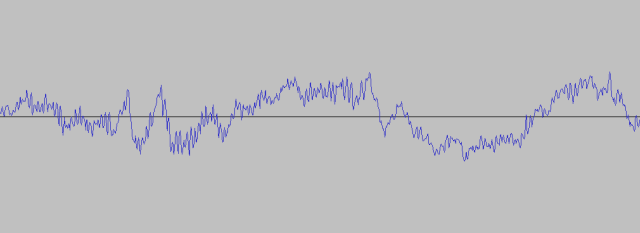
Part of a typical analog waveform (about 30 milliseconds of "Good Vibrations")
Digital technology works differently. Instead of a continuous range of possible values, digital values are limited to a finite set of possible values. For the most basic circuits, this is the familiar “zero” and “one” of binary arithmetic, represented as two specific values (say, zero and five volts) in a circuit. Values near zero (for instance, values up to 0.5 volts) are considered “low” (or “zero”), and values near five volts (say, anything over 4.5 volts) are considered “high” (or “one”). Values between 0.5 and 4.5 volts are not guaranteed to be either value, and should be avoided.
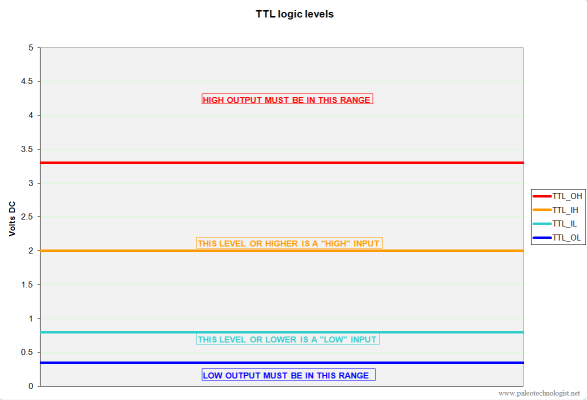
TTL voltage levels (click for larger)
Digital signals, therefore, are always either zero or one. Information is passed not by directly copying a microphone’s movements into changes in voltage, but by describing those changes using zero and one. Such descriptions using a small set of values have been around for years — the dots and dashes of Morse Code have been used for over 150 years! Similarly, every wire carrying a digital signal switches between “high” and “low” values, producing a waveform that looks very different from an analog signal…
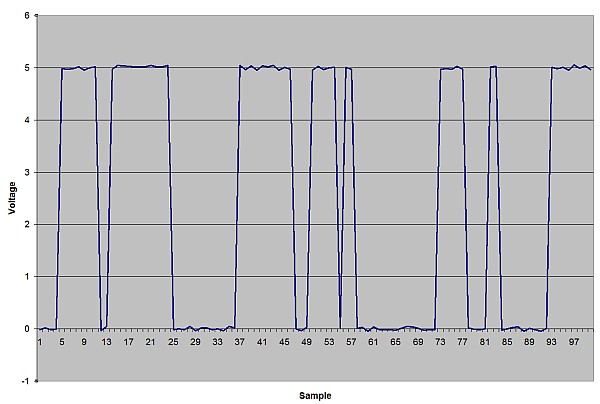
A (synthetic) digital signal, including a bit of noise. (Click for larger.)
At first, this seems very restrictive. How can you convey the delicate nuances of, say, a Chopin nocturne or the expansiveness and majesty of Tchaikovsky’s 1st piano concerto, if the music is broken up into little pieces like this?
The answer is that digital signals, although “zero or one” by themselves, can describe more complex signals. An analog signal from a microphone is “digitized” into a specific range of values. For music played by a CD player or typical mp3 player, sixteen bits per sample are used, meaning each sample of the signal is broken down into 2^16, or 65,536, possible values. A series of sixteen “bits,” each zero or one, is sent to represent each sample. Do this 44,100 times per second for each channel (left and right), and you have enough information to put the original signal back together almost exactly as it originally was. (If you want greater precision, use more bits and/or sample the signal more times per second. DVD-audio players can play back 24-bit music with up to 192,000 samples per second.)
This is much more accurate than any amplifier or speaker could ever hope to reproduce, by the way, despite what some audiophiles say. Discussions about the minutiae of amplifier design aside, there is no good reason to categorically dismiss digital recording technology. Use enough bits of precision and a fast enough sampling rate, and something else in the chain (the speakers, the wire, human ears, etc) will become the weak link.
With this understanding of what digital technology is, the benefits are easier to describe. The central point of digital technology is that it can describe any information — music, temperatures, Shakespearian sonnets, pictures, videos, etc. — as bytes (standardized, 8-bit characters). This seemingly trivial point is the key to all of the digital magic of the past few decades. Once a piece of information (say, a song) has been digitized, it can be treated like any other piece of information. It can be copied over and over — perfectly, without any degradation whatsoever. It can be emailed, stored for later use on a hard drive, archived, made searchable, analyzed, used as a ringtone, shared (I won’t get into legalities here), and played back over a network. All of this is possible because, to a computer, there is no difference between the characters that make up this song and those that make up an email, spreadsheet, database, program, or picture.
If signals were stored in analog format, specific conversions would have to be performed on each type of signal (audio, video, etc), before they could be copied to another computer, sent over a network, etc. Once information has been digitized, however, it is all fundamentally a series of bytes — and can easily be stored, recalled, transported, encrypted, decrypted, combined, analyzed, and sorted. Without this functionality, the Internet wouldn’t be possible in anything resembling its current form.
That’s what makes the “Digital Revolution” revolutionary — and that’s why it’s so important.