Computers generally don’t solve problems the same way humans do.
Take Sudoku, for instance. A human Sudoku player will usually look for patterns in the existing numbers, looking for possible spots to place a 1, 2, 3, etc. Or maybe they will notice that a particular square has everything but a 7 and 8, with one in line with another 8, and will deduce what goes where based on that. We look for what makes sense, and try to piece together a rational solution based on logic and observation.
Such relatively sophisticated, creative, intuitive heuristics don’t always represent the easiest way to solve a problem using a computer. Sometimes a simple exhaustive search (one that my former Calculus teacher called the “Brute Force and Ignorance” approach) is best. After all, modern computers have a lot of brute force to bring to bear!
How could one most simply describe how to solve a Sudoku puzzle, given that the solver could follow instructions exactly — and was really, really fast at carrying them out? One method would be to try every single possible combination until something works, backtracking when you come across a dead end. Try to place a “1” in the first blank square, and check to see if there are any conflicts. If not, good — write it down and solve the remaining puzzle. If no such solution exists, or the “1” doesn’t fit, erase it and try a “2” there — and so on. This is the algorithm presented in an excellent recent Computerphile video about how to solve Sudoku in Python.
For some problems, like Chess, this kind of approach is untenable, since it won’t finish before the expected heat death of the Universe. Chess, while nowhere near as complex as Go, still has something like 10^120 possible games.
For Sudoku, however, this works surprisingly well. Most numbers that are tried are dead ends — but if so, they are usually found out quickly. If the algorithm successfully placed a “1,” for instance, it will still blindly try to place a “1” right next to it, since that’s the next step. This will fail, but it will fail quickly, allowing the algorithm to advance and try a “2” and then “3” until it finds something that sticks. No human would check all of these clearly-wrong branches — but they also take much longer to check the plausible ones.
How long would such a dumb, brute-force algorithm take to solve a Sudoku? I wasn’t sure — maybe years? So I tried programming it in C. (Here is the source file.) The example puzzle from the video was solved in about 120 milliseconds on my (ten-year-old but still modern-ish) PC, after having searched 37,652 possible number placements. Not bad!
Next, I looked for a real challenge, and came across what is said to be the world’s hardest Sudoku puzzle…
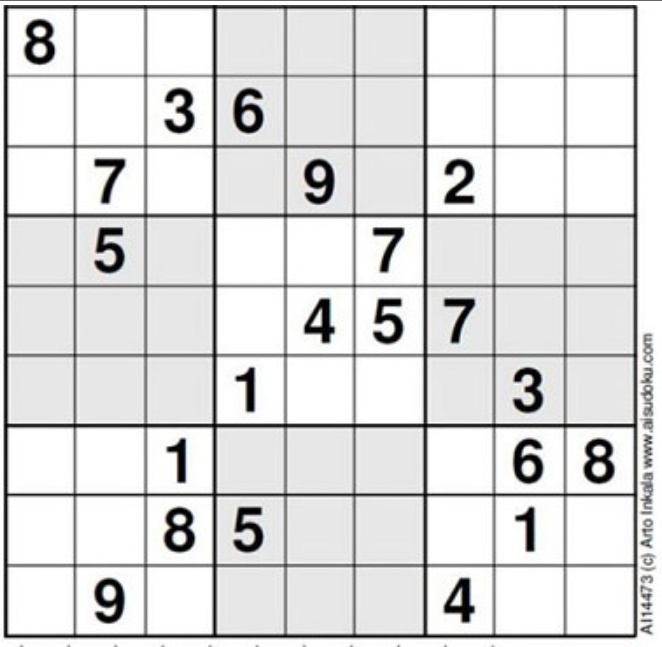
This is a nasty one! Nothing obvious jumps out at you, although in a few cases, you can narrow down the choices a bit and start to make progress. I entered in the data and re-ran the program.
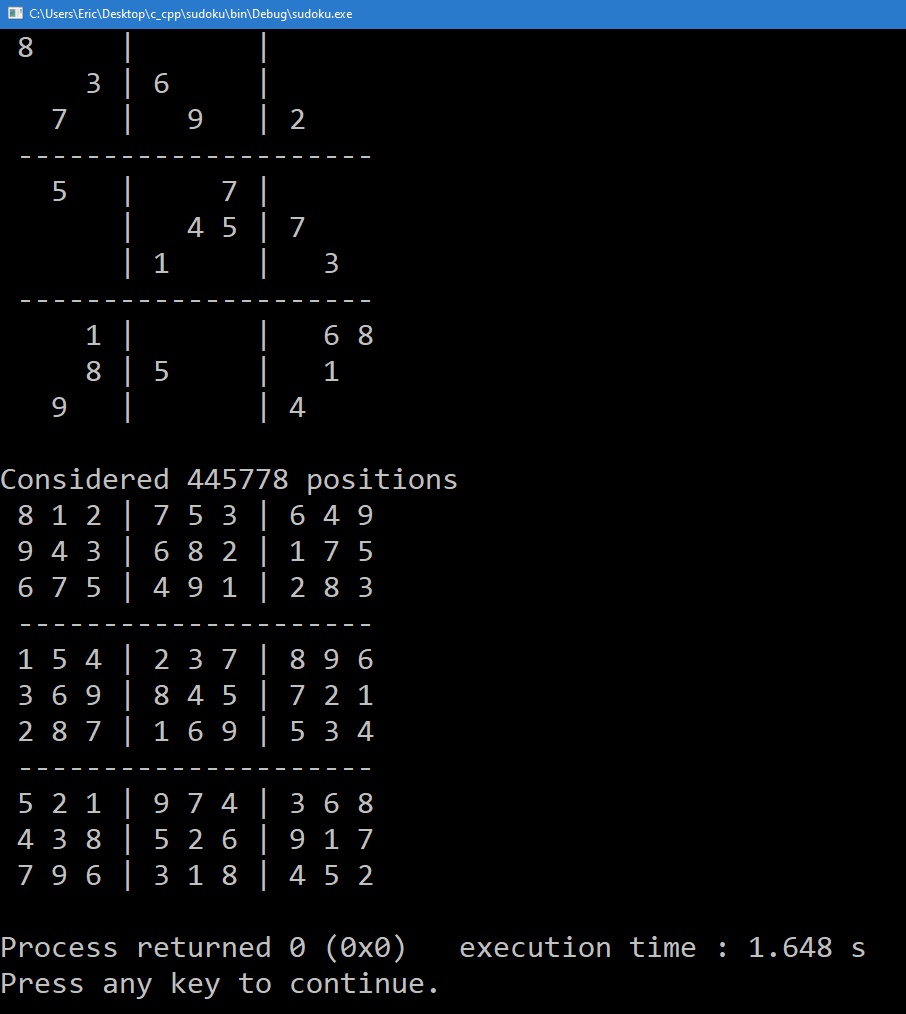
This puzzle put up a good fight — there was actually a noticeable pause before the solution displayed — but roughly 1.65 seconds (and maybe something like five billion clock cycles) later, the unique solution popped up:
Lots of progress has been made on many fascinating, important problems by coming up with new algorithms. QuickSort, hashes, distributed computing, heuristics, and similar advancements have made efficient search engines possible. Clever branch-and-bound approaches have enabled Chess (and probably Go) engines to outplay any human.
But sometimes, all you really need is a big hammer.