Although we’re all familiar with the flat Mercator map of the Earth, it exaggerates areas at high latitudes. More importantly for navigation, it also suggests very inefficient routing — routes calculated by taking the starting and ending latitude and longitude and using linear interpolation to find intermediate waypoints works well enough for low latitudes, but could end up suggesting a route that’s more than 50% longer, at high latitudes.
Consider a hypothetical flight from Murmansk (ULMM) to Anchorage (PANC). Although both cities are between 60 and 70 degrees north latitude, the shortest path between the two passes almost directly over the pole. In contrast, drawing a straight line between the two on a Mercator projection would imply a best path across Scandinavia, passing north of Iceland, then over Greenland and most of Canada before approaching Anchorage from the East.
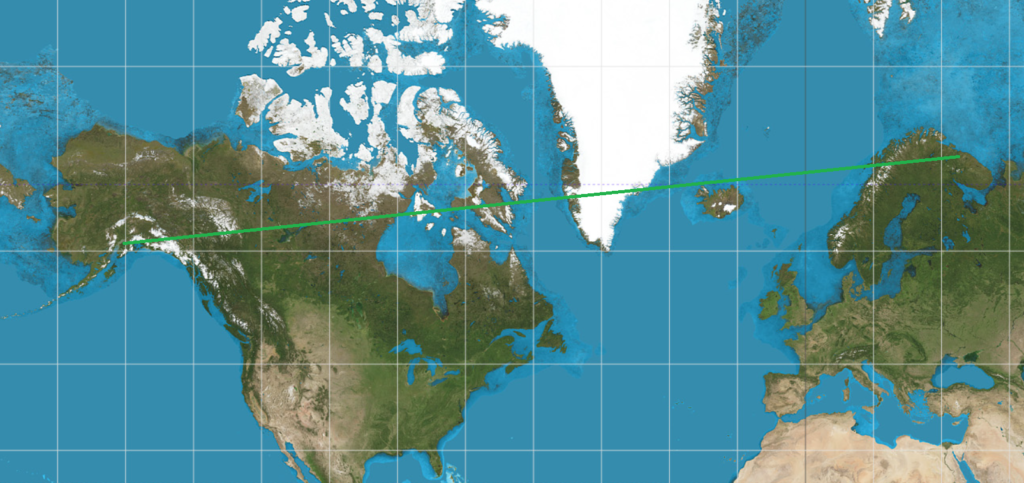
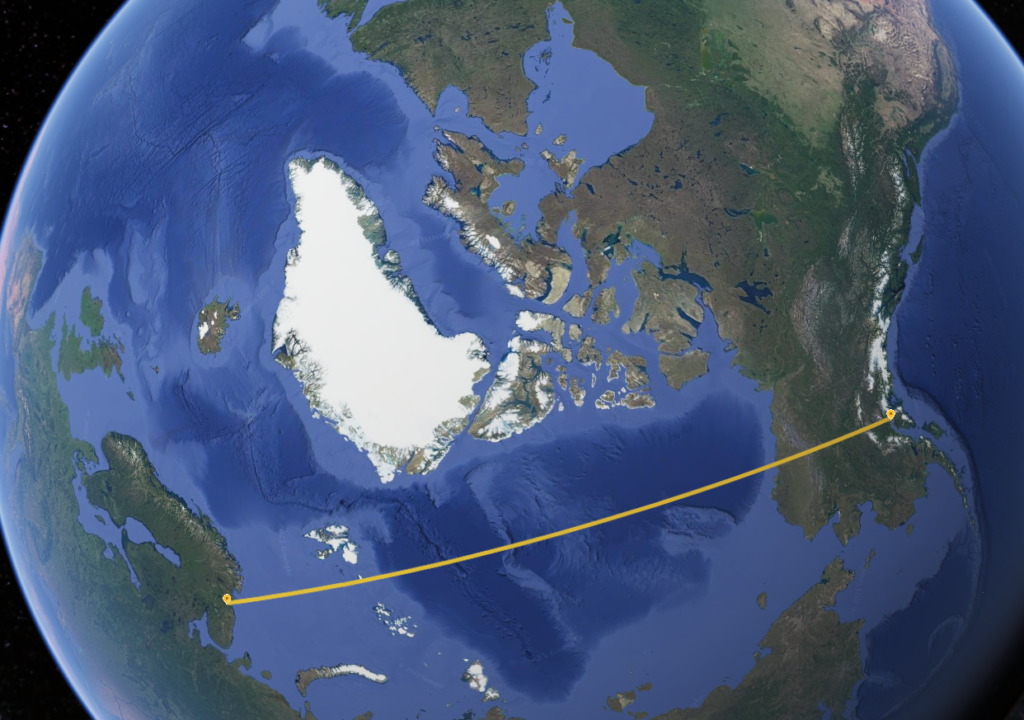
So Great Circle routes are faster — but how can you calculate them? It seems complicated — but a key observation can help. The Great Circle route is the shortest route between two points along the Earth’s surface because it is the projection of the actual shortest path through space.
With this insight, we have a plan of attack:
- Consider the Earth to be a unit sphere. This is slightly inaccurate, but it works well enough.
- Convert the starting and ending points to XYZ Cartesian coordinates;
- Choose how many points to interpolate along the route;
- Interpolate these linearly (directly through XYZ-space — through the body of the Earth);
- Extend the distance from the origin of each point so it sits on the unit sphere
(I.E. compute the distance of the 3D point from the Earth’s core, and extend it to 1.0 length); - Compute the latitude of each point as arcsin(z), and the longitude as arg(x+yi).
While this method doesn’t split the path into equal length segments, it gets most of them fairly close, with segment distances varying by 20% or so. If desired, this could be adjusted by changing the points selected along the initial linear path.


