To The Moon

Posted on 2014-01-20 by M. Eric Carr

Dogecoin has got to be the most Internet thing ever. It’s difficult to understand just what Dogecoin is without a solid understanding of recent Internet lore, though, so a bit of background information is helpful. Specifically, your two prerequisites are an understanding of both the recent “doge” meme and of cryptocurrencies.

One of the most popular memes of late 2013 is the “doge” meme. This meme consists of a picture of a Shiba Inu dog named Kabosu (looking at the camera with the fascinated, excited-yet-cool expression that Shibas tend to have) along with poorly-spelled-but-enthusiastic expressions (“such doge!” “wow”) in colorful Comic Sans.

dogeThis meme has been making the rounds since late 2012, and took off in 2013. About a month ago, doge served as the inspiration for a new cryptocurrency.

Cryptocurrencies (most famously, Bitcoin) are a recent attempt to reinvent the idea of currency. As Douglas Adams so skillfully points out in The Hitchhiker’s Guide series (when some of the characters start using common leaves as currency), one of the fundamental drivers of value is scarcity. It’s the basic law of supply and demand. Cryptocurrencies are a grand experiment in the democratization of currency. With the loss of the “gold standard,” traditional currencies like the US dollar are “fiat currencies” — the value of which is determined by the expectation that they will be able to be traded for tangible goods or services.

So, to be viable as a currency, you need scarcity and an expectation that others will accept your currency in exchange for goods or services. By their nature, cryptocurrencies have the former. With Bitcoins now trading for close to $1000 each, it is becoming evident that the economic pump can be primed, and that such currencies can reach critical mass and acquire value.

The inherent scarcity of cryptocurrencies comes from mathematics and the idea of “proof of work.” In a nutshell, millions and millions of complex computations are required in order to find a suitable numerical “block” representing new currency. This currency can then be securely traded to others via public-key cryptography — in a public, verifiable, nonrepudiable way. As a bonus, these transactions can also be made anonymously, with new account numbers being able to be generated at will. Transaction histories can eventually be traced back to their origins (since every transaction is public), but laundering such currency can be fairly straightforward: if even one link in the transaction chain cannot be verified, the final recipient is now anonymous.

So, basically, cryptocurrencies are generated by performing lots of complex calculations on very fast computing hardware (modern CPUs and graphics cards are quite good at this), and can be traded to others electronically in a secure, reliable, anonymizable way.

This sets the stage for Dogecoin, which started out as a spoof and still has an irreverent feel to it. The algorithms for “scrypt”-based cryptocurrencies are open source, meaning that anyone is free to take the algorithm and use it to make their own currency scheme. (Convincing others of the value of this currency, of course, is the hard part.) Some users of the Internet discussion board Reddit decided to create a new, meme-based currency to “tip” fellow Redditors for useful comments and link contributions. Thus, Dogecoin was born in December 2013.

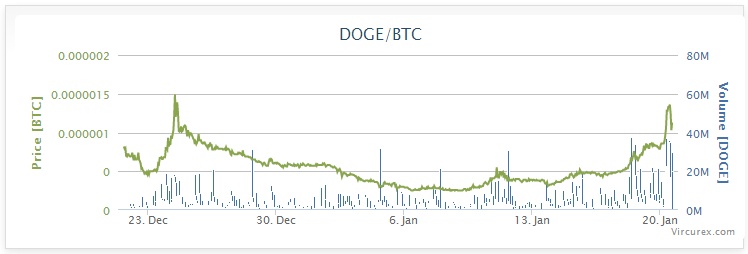
Since Dogecoin is still a small-cap currency (with a total value somewhere in the tens of millions of USD), its value has been rather volatile. Recently, the volatility has been in a dramatic upward direction, raising the hopes of “shibes” (Dogecoin enthusiasts) that the currency is headed “to the moon.”

dogecoin_moon

I’ve been mining Dogecoin for a while now, and have close to 60,000 Doge. At current prices, this is about US$77 (although it would have been worth less than half of that a week ago). Next week or next month, who knows?

doge_chart

 

Such moon
Wow   So crypto

 

 

 

 

Posted in Current Events, Digital Citizenship, Internet, Math | Tagged , , , , , , , | Leave a comment

Numbers Of Unusual Size

Posted on 2013-12-31 by M. Eric Carr

Mintoris Basic just keeps getting cooler. It already had support for most Android peripherals such as sound input and output, accelerometers, and many other nifty features. Now it has support for arbitrary-precision decimal numbers, including Integers Of Unusual Size™.

As with pretty much all things Mintoris Basic, the large numbers are very straightforward to use. Here’s code to generate Fibonacci numbers, for instance:

a$=”1″
b$=”1″
print a$
print b$
Top:
a$=bigadd(a$,b$)
print a$
b$=bigadd$(a$,b$)
print b$
wait 1
goto Top

I gave up after the numbers got too big to fit on the screen on my Acer tablet — over 4,000 digits!

It supports arbitrary-precision decimals, too.

Posted in Android, BASIC, Coding, Digital, Math, Tools | Leave a comment

Longer than long

Posted on 2013-11-05 by M. Eric Carr

Sometimes you need to use really big numbers — and 32 bits just won’t cut it.

Fortunately, the gcc compiler has this covered; its “long long” type supports signed and unsigned 64-bit integers. The difference is huge — whereas unsigned 32-bit integers are limited to 0-4,294,967,295, 64-bit integers can go all the way up to 18,446,744,073,709,551,615.

These numbers can be used in C as shown in this example:

#include <stdio.h>
int main(){

//Variable declaration
unsigned long long int myNumber = 1;
int power;

//For loop
for(power = 0; power < 63; power++){
printf(“Power: %d      Number: %llu\n”,power,myNumber);
myNumber = myNumber * 2;
}//for

return(0);

}//main()

Posted in C, Coding, Linux, Math | Tagged , , , , , , | Leave a comment

PIC output characteristics

Posted on 2013-10-31 by M. Eric Carr

In order to automate several functions at home, I am in the process of designing a low-speed home automation network. Since one of my primary goals is to have individual nodes be as low-cost as possible, I have decided on a clocked multi-master serial bus interface. Since the specifics of the interface (pullup resistor strength and signaling speed, mostly) will depend on the output characteristics of the individual nodes, some testing of a representative PIC microcontroller (a 12F683) is needed.

My testing protocol (if I can even call it that) is informal and straightforward. A capacitance, representing a conservative estimate of the capacitance of a length of RJ12 cable, is connected to an output from a PIC microcontroller. Since the network will be open-drain to avoid contention issues, a 270 ohm resistor will be used (digital outputs on a PIC are rated to source or sink 20mA max, so the pull-up resistance should be no less than 250 ohms. Power consumption is not a major concern, and a value close to the lower limit will allow faster rise times and therefore faster signaling.)

The experimental setup…

The first experiment was at full speed (running on the internal 8MHz clock): a 500ns pulse, with the pin being actively driven high and low. No capacitance was added, and no pull-up resistor was used.

01_500ns_no_load_active

500ns pulse, no load, active high/low

Next, a 270 ohm pull-up resistor was added, and an open drain configuration was used (with the pin always either driven low or tristated, never driven high). This will prevent an overcurrent condition on the bus, should two devices assert different values at the same time.

03_500ns_270r_od

500ns pulse, 270 ohm to Vcc, active low / open drain

Next, 100pF capacitance was added. This had little or no effect on the actively-driven falling edge, but did start to affect the pulled-up rising edge.

500ns, 270 ohm pull-up, open-drain, 100pF load

Next, the capacitance was increased to 1nF. This resulted in the voltage taking most of the 500ns pulse time to recover.

500ns pulse, 270 ohm pull-up, open-drain, 1nF loading

Because of this, I decided to slow the pulses down. I first tried 5us pulse widths, but the capacitance still couldn’t be increased past 1nF or so.

5us pulse, 270 ohm pull-up to Vcc, active low / open drain, 1nF loading

5us pulse, 270 ohm pull-up to Vcc, active low / open drain, 3nF

Finally, I settled on a 50us pulse time. This allows data transmission at up to 20kb/sec with a reasonably clean signal, even with 10nF loading. 6-conductor flat satin cable is stated by Black Box to have a characteristic capacitance of 22pF per foot. In standard units, this is 22pF per 304.8m, or about 72.2nF per meter. Since I plan on having about 25m of cable in the network to start (and perhaps as much as 100m eventually), this should result in a total cable capacitance of between roughly 1.8nF and  7.22nF.

50us pulse, 270 ohm pull-up to Vcc, active low / open drain, 10nF loading

Here is a detail of the risetime at 10nF, showing a risetime of about 10us. By sampling past the halfway point of each bit period, the signal should be stable even with 10ns loading. 20kb/sec should therefore be fine. I’ll probably run it at 19,200 for nostalgia if no other reason.

50us pulse, 270 ohm pull-up to Vcc, active low / open drain, 10nF risetime (detail)

These risetimes could, of course, have been calculated in terms of time constants (tau = RC), but it’s always nice to see actual results produced by actual hardware. One particular concern that I had was whether the PIC’s tristate functionality could really be relied upon to work this way, rather than as a relatively slow way to set up pin functionality upon initialization. It does indeed work nicely — apparently just as fast as actively toggling bits (although controlling both tristate and pin value would require swapping memory banks, which takes a few cycles.) For this test, the software simply remains in the TRISIO bank.

 

Posted in Analog, Digital, Electronics, PIC Microcontrollers | Tagged , , , , , , , , , | Leave a comment