Winging It

Posted on 2021-12-14 by M. Eric Carr
Finally on approach to Anchorage 07R.

I didn’t think it would get here.

While grading final exams and term projects, I often set up a long-haul flight in X-Plane as something to check in on to take a break now and then. I thought about using my usual Zibo mod 737-800, but noticed an ex-NASA “747-100” in the fleet listing.

“Oh — that old thing?” The dispatcher pulled a clipboard from the wall. “Ex-NASA 747-100 Space Shuttle Carrier…” He looked at the plane for a moment, seemed about to say something, then thought better of it. “Not sure where we downloaded it from, honestly. I think it’s been — no, being — refurbished to go to a museum somewhere. It needs to go to Anchorage for testing, next. We think we can get the FAA guy to sign off on a ferry permit if you want…”

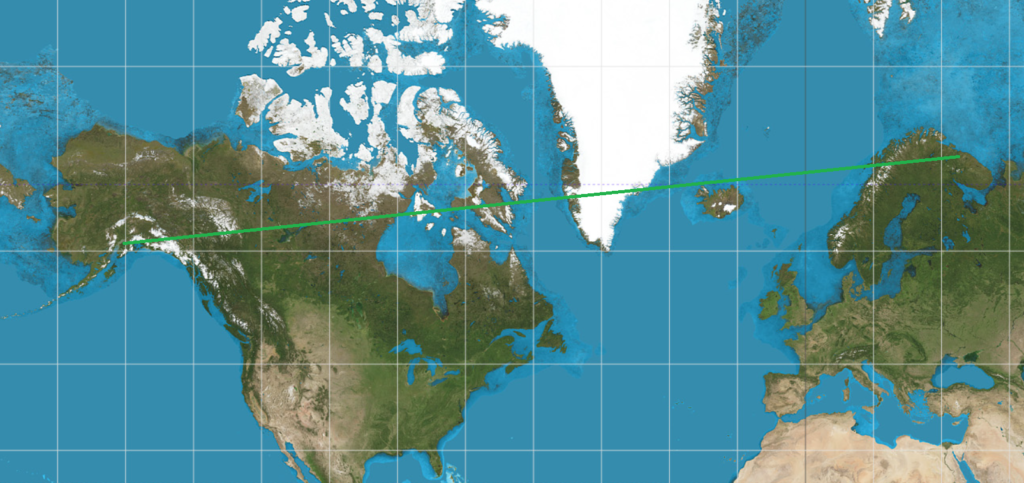
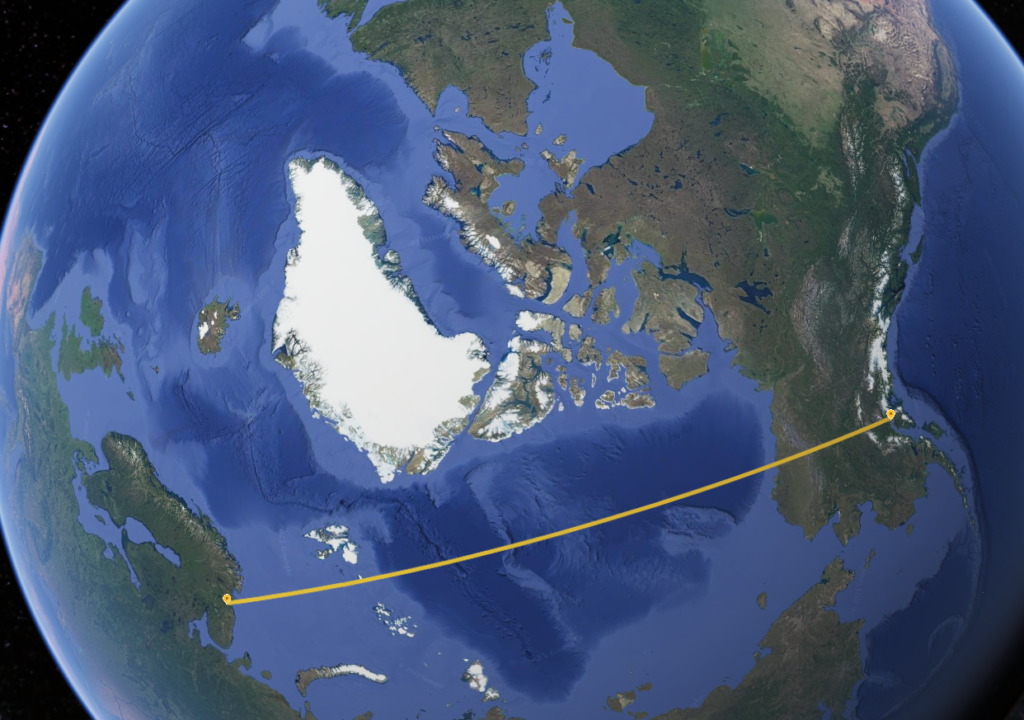
Sure — why not, I thought. They fly 747s from Dulles to Anchorage all the time. Or at least, it’s a plausible route. If it’s really a -100, it will probably be VOR navigation only unless it has an INS. In that case, we could cheat and route directly to an initial approach fix. (I’m not a stickler for realism in routing, since I fly offline.)

I loaded the plane and was greeted by the flight deck you see above. This, plus the lack of Flight Engineer’s station, told me this was probably a -400, or at least using -400 glass-cockpit controls, with the steam gauges only as backup.

No problem, I thought. I can fly either style, but my life just got easier. And it did — sort of. I turned on the battery and lit the APU. Once it was up and running, I set it up to run the electrics. I then turned on the APU bleed and went to turn on the packs — but the switches were disabled. Maybe they need the engines to be running…?

Starting the engines was fun — the secret combination seemed to be to turn the fuel on and then pull the starter switch until it lights up. Kind of backwards from the 737 (fuel is the last step there, after 25% N2), but whatever. Four good engine starts. I was worried we wouldn’t have an EPR gauge for #2 , since it was acting weird and reading full scale when off and at idle, but it seems to work when the engines are at power. Eh — we’ll write it up for the team at Anchorage.

Once all four engines were running, I went to switch the engine bleeds on and turn on the packs. No dice — the switches were off and probably not modeled. After trying everything I could think of, I had a chat with Maintenance about it, and asked them to fix it. I switched on the Inertial Navigation units, so they’d have a chance to align.

I looked at the overhead panel. None of the hydraulic systems were on, although I’d tried pressing the relevant buttons. #4 was showing System Fault. Also, the hydraulic brake pressure was at zero. Nice. That should make for an exciting landing.

Fuel? The center panel says we have 150 (metric) tons. It doesn’t say which tanks this is in, or how much is in each, or what the fuel valve configuration is. That’s all on the Fuel screen, and the button naturally doesn’t work. Eh — hopefully the fuel guys are more competent than they looked. We’ll hope it’s fueled and configured correctly, and send it.

The maintenance guy stuck his head in the cockpit. “We can’t get the bleeds to work, but we found a bunch of oxygen canisters and bomber jackets for you guys so you can run unpressurized. Just pretend you’re flying a B-17. And don’t tell the FAA guy, hey?”

Well, that will be a new experience. Hopefully they’ll disable the passenger oxygen mask drop mechanism, because we don’t have any controls for that, either. Next, I looked at the Flight Management Computer (FMC). It looked professional enough until I started trying to get it to do anything. Oh, well. Old-school VORs it is. We have GPS/INS navigation, but no way of entering waypoints — or any way to tell what the names of the ones on the screen are.

By now, the IMCs had aligned (suspiciously quickly). I decided not to complain — maybe they’re GPS-assisted or something — and tried to put together a semblance of a takeoff checklist:

  • Flaps: I dunno. Let’s try 10. That’s what the chart would say if we had one, right?
  • Autobrake: (We seem to have the world’s only 747 without autobrakes. Nice.)
  • Flight Directors: On. (Oh, hey — they work!)
  • Heading: Set to 011
  • Altitude: Set to 32,000

With the definite thought that there’s no way I’d be taking this disaster into the air if this weren’t a simulation, I shrugged, advanced the throttles, and released the brakes, and watched as the 747 performed a beautiful, graceful takeoff almost on its own. That’s a relief, I thought, since we didn’t have any trim setting guidance either, so that was also a guess.

I pulled up the gear and flaps, engaged the autopilot and got it pointed towards the first VOR, then looked for the OBS dial to set up a direct course. Weirdly, I couldn’t locate it by the time we had passed the VOR, so I tuned to the second one and continued steering it in Heading mode. After a very thorough fifteen-minute search, I realized that the OBS dial didn’t exist. So we can tune VORs, but we can’t tell the plane which radial to use. Sigh. Time to add in some keyboard commands to set it and hope that works. (How the hell are we gonna fly the ILS approach, otherwise?)

Hacking in OBS functionality with keyboard commands worked — but then the plane seemed to get confused. The HSI display on the 744 (and this Frankenplane’s nose was a 744, even if the back end was a 741 and who knew what the wing and engines were from) only showed a sliver of the entire circle, for visibility. What I couldn’t see was that the arrow I had aligned with the VOR was actually the backcourse arrow. The plane, thinking it was being asked to follow an easterly course, wavered and then began a turn back east before being put back on Heading mode. Bad plane. No cookie!

Maybe it’s reverse-sensing? Still in Heading mode, I turned the OBI 180 degrees. This side had a larger arrow — which would have been obvious on a full-scale display. Mystery solved. We may not have full automation, but we can track radials, now.

Well, sort of. The nav display doesn’t seem to make sense. Planes generally don’t quite point in the same direction they’re going, of course — they have to turn slightly (crab) to account for wind drift. This display had a heading bug and indicator, a track direction indicator, and a VOR radial indicator, no two of which generally agreed during the flight unless going directly upwind.

Even somewhat-accurate navigation will still get you from VOR to VOR, though, so I was able to get it to slowly make its way across the US and Canada, headed for Anchorage. It soon reached its cruise altitude of 32,000′, which was when I discovered that the autothrottle didn’t work well, either. The plane levelled off just fine, but kept increasing and decreasing the throttles every few seconds, chasing small variations in wind. I turned it off and set the throttles manually, and almost didn’t have to touch them for the rest of the cruise.

It was while setting the throttles for cruise speed that I noticed the single most iconic thing about this plane. Ships have their bell as the “soul” of the ship. This mess of a 747-whatever had its very own factory-seconds indicated airspeed (IAS) gauge, centrally placed to inform its hapless crew that while they may be flying the Queen of the Skies, this particular Queen was built on a Friday afternoon and modified on a Monday morning, so keep your eyes open.

That “350” should be “320.” At least, if we can trust the main IAS tape.
250-300-350-400 would make more sense, but that’s not how it works, unfortunately.

It’s glorious, and explains everything about this poor plane.

I managed to get it the rest of the way to Anchorage and get lined up for the 07R ILS, and it made a beautiful landing — as with the takeoff, almost completely by itself. The 747 — even a broken, confused one — is an amazing machine. The brakes even somehow worked, which was surprising given the lack of hydraulic pressure.

But yeah. Don’t buy jumbo jets from shady NASA guys in trench coats, kids. I’m flying the Zibo back East and sending this bird to Maintenance before something else breaks.

Posted in Flight Simulator, Troubleshooting | Tagged , , , , , , , , , , , | Leave a comment

Arduino On The Go

Posted on 2021-11-29 by M. Eric Carr

Don’t look now, but that smartphone you’re carrying might be faster than your desktop. Even if not, modern smartphones are certainly capable enough to be used for many computing tasks traditionally left to desktops and laptops.

Smartphones typically have a single USB port — either MicroUSB or USB-C. For something like ten years now, these have generally all been capable of “USB On-The-Go” (USB-OTG) operations, where the smartphone switches functionality from USB device to USB controller. Plug in an inexpensive USB On-The-Go adapter, and your smartphone can access most of the same USB devices your desktop and laptop can. They can read and write flash drives, use USB keyboards and mice — and even program Arduino-compatible boards.

A Samsung A71 5G programming a TTGO T-Display via ArduinoDroid.
This is the whole setup — no PC is needed (for simple sketches, anyway.)
Even the Bluetooth keyboard is technically a luxury — if a very useful one!

I recently used a similar setup for troubleshooting a faulty speed sensor on a friend’s boat. A smartphone and Bluetooth keyboard are portable enough to use on board, where a laptop would be awkward and a desktop almost impossible to use.

I’ve started carrying a USB On-The-Go adapter with me. I figure if I’m already carrying the supercomputer, I might as well bring a USB port for it along.

Posted in Android, Arduino, C, Coding, Toys | Tagged , , , , , , , , , , , , | Leave a comment

Computer Speed Comparisons, Part 1: Integer Math

Posted on 2021-10-31 by M. Eric Carr

When comparing the performance of computers across several generations (and often, several orders of magnitude in speed), it can sometimes be challenging to find an appropriate computational task that is scalable across a large enough range. Tasks that can take hours on a machine from the 1970s or 1980s (or earlier) can sometimes only take fractions of a second on a modern PC, skewing the results due to noncomputational overhead and quantization errors.

Fortunately, there exist several types of task that make at least limited speed comparisons possible. One such task for measuring integer-operation speed is the computation of the sums of the first 10^N prime numbers.

Prime numbers occur regularly enough to be a good benchmark, and sums of the first N primes are well-known, allowing verification of not only speed but algorithm correctness. This is a task that can both be accomplished by almost any computing device created — and yet can challenge even modern supercomputers. The task scales itself to the processor speed, even over many orders of magnitude.

The algorithm chosen is a simple not-quite-naïve for loop, checking each odd integer for divisibility by the odd numbers up to and including its square root. More sophisticated algorithms such as using the Sieve of Eratosthenes can speed up the calculation — but the idea is to use the simplest reasonable implementation possible, so it can be run on very simple machines. This way, the computing speed of vintage devices can be compared to modern ones — sometimes with fascinating conclusions. Machine-internal timing is used where possible.

Here is the C version: Primespeed.c

Here is the FreeBasic version: Primespeed.bas

Timex/Sinclair 1000 BASIC version.
(Screenshot only for now; system still needs upload capability)

One interesting observation is that (for most setups where printing the data doesn’t take appreciable time) summing 10^(N+1) primes seems to always take about 33.3 times as long as summing only 10^N primes. This suggests a uniform way to scale the comparisons logarithmically, since each “level” (summing ten times as many primes) represents 33.3x as much computation. Scores for each machine under this scaling should be relatively consistent whether they’re calculating primes for a minute, an hour, or a week.

The Sinclair took about 175 seconds to calculate the sum of the first 100 primes, and 2526 seconds to compute the first 1,000. Assuming that each 10x increase in the number of primes computed represents a 33.3x increase in the number of computations, it’s reasonable to expect it to compute the sum of the first one million primes in about 175*(33.3^4) seconds (about 215.2 million seconds, or about 6.82 years.)

A good metric should be logarithmic for convenience. A reasonable one might be the log10 of the number of primes each machine would be expected to compute in 1000 seconds. With that, here are the results for various devices ranging from the 1980s to the present:

  • Timex/Sinclair 1000: 1,000 primes in 2,526 seconds: 2.74
  • TRS-80 Model 100: 10,000 primes in 3758 seconds: 3.62
  • ESP32: 10,000,000 primes in 24,629.97 seconds: 6.09
  • PocketChip: 1,000,000 primes in 460.38 seconds: 6.22
  • Northlight (Core i7/980X): 100,000,000 primes in 12,706.8 seconds: 7.27
  • Scientia (Core i9/9900): 100,000,000 primes in 9347.09 seconds: 7.36
  • Samsung A71 5G phone: 100,000,000 primes in 7099.7 seconds: 7.44

Note that these are logarithmic scales; each additional point means roughly a 10x speedup.

Some interesting observations:

  • The interpreted-BASIC machines are slowest, as was expected.
  • WinFBE’s compiler seems to be slightly better at integer ops than gcc.
  • Single-thread performance has not gotten significantly better in recent years.
  • If the slowest machine (the Sinclair) is compared to the speed of a literal snail, the fastest devices tested (desktops and a smartphone) would be about as fast as airliners.
    …but most surprisingly,
  • My Samsung A71 5G smartphone beat everything, including the desktops, and is something like 50,000 times as fast as the Timex/Sinclair, at computing primes. That’s not surprising — but I wouldn’t have guessed it would outrun a modern Core i9(!)

Finding the first ten primes in my head took me about twelve seconds as I was going to sleep. This would result in an equivalent score of about 2.26 (but wouldn’t scale very far.)

Posted in BASIC, C, Coding, Math | Tagged , , , , , , | Leave a comment

The Short Way Around

Posted on 2021-09-29 by M. Eric Carr

Although we’re all familiar with the flat Mercator map of the Earth, it exaggerates areas at high latitudes. More importantly for navigation, it also suggests very inefficient routing — routes calculated by taking the starting and ending latitude and longitude and using linear interpolation to find intermediate waypoints works well enough for low latitudes, but could end up suggesting a route that’s more than 50% longer, at high latitudes.

Consider a hypothetical flight from Murmansk (ULMM) to Anchorage (PANC). Although both cities are between 60 and 70 degrees north latitude, the shortest path between the two passes almost directly over the pole. In contrast, drawing a straight line between the two on a Mercator projection would imply a best path across Scandinavia, passing north of Iceland, then over Greenland and most of Canada before approaching Anchorage from the East.

It looks convincing, but the Flat Earth path will take a lot longer…
The Great Circle route. Seen on a globe, this is the obvious shortest path.

So Great Circle routes are faster — but how can you calculate them? It seems complicated — but a key observation can help. The Great Circle route is the shortest route between two points along the Earth’s surface because it is the projection of the actual shortest path through space.

With this insight, we have a plan of attack:

  • Consider the Earth to be a unit sphere. This is slightly inaccurate, but it works well enough.
  • Convert the starting and ending points to XYZ Cartesian coordinates;
  • Choose how many points to interpolate along the route;
  • Interpolate these linearly (directly through XYZ-space — through the body of the Earth);
  • Extend the distance from the origin of each point so it sits on the unit sphere
    (I.E. compute the distance of the 3D point from the Earth’s core, and extend it to 1.0 length);
  • Compute the latitude of each point as arcsin(z), and the longitude as arg(x+yi).

While this method doesn’t split the path into equal length segments, it gets most of them fairly close, with segment distances varying by 20% or so. If desired, this could be adjusted by changing the points selected along the initial linear path.

Posted in Algorithms, Aviation, Coding, Math | Tagged , , , , , | Leave a comment