(This is the first of a planned series of articles on interesting topics in mathematics. Don’t worry, though; there won’t be a quiz. The whole idea is to show the fun side of math!)
One of the more interesting topics in math (for me, anyway) is emergent complexity. Often, very simple systems can lead to complex behavior. Fractals such as the Mandelbrot Set are a good example of this. Another example is Conway’s Game of Life.
Discovered / invented by Dr. John Conway in 1970, Life is a specific cellular automaton: a set of rules for updating the states (“alive” or “dead”) of a rectangular grid of cells (Conway apparently did some early investigations using a checkerboard.) Starting from a given “seed” configuration, the following two simple rules are repeatedly applied (to all of the cells at once):
- If a “live” cell has exactly two or three neighbors, it remains “alive” in the next generation. Otherwise, it “dies” (potentially to be reborn again later).
- If a “dead” (or “empty”) cell has exactly three neighbors, it becomes “alive” in the next generation. Otherwise, it remains empty.
These two simple rules lead to all sorts of interesting behavior. Some configurations quickly die out; others quickly evolve into stable “still life” configurations. The most interesting ones, though, can drift away across the plane, grow without bound, or play out in a chaotic manner for hundreds or thousands of generations before becoming stable. Here are some examples:
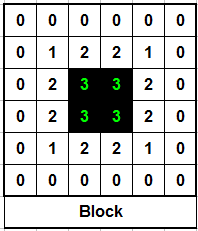
A “block” of four squares will remain exactly as it is — a classic example of a “still life”. Each live cell has three live neighbors; no empty cell has more than two — therefore, no cells ever die or are born.
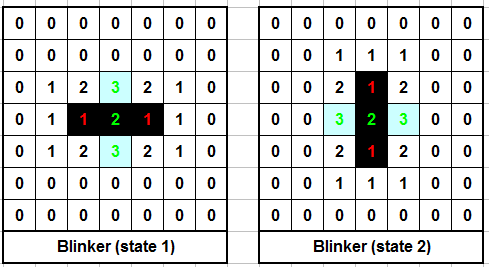
Three cells in a row will oscillate between horizontal and vertical configurations — becoming a “blinker.”
A diagonal row of cells will evaporate from each end…
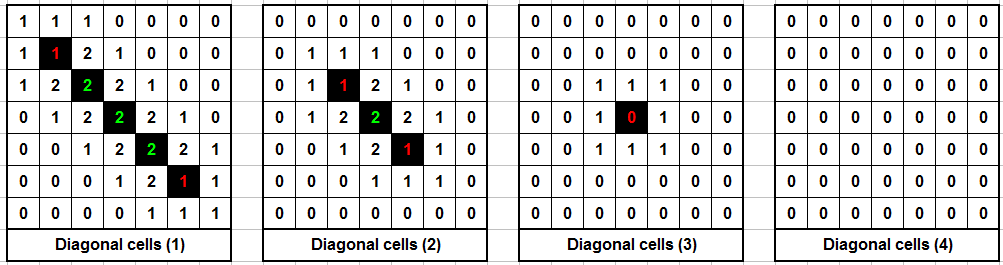
…but a diagonal row of cells “anchored” at both ends remains stable.
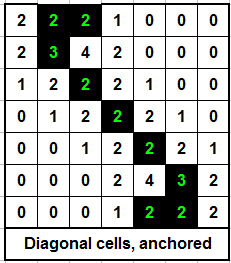
These are somewhat interesting — but the beauty of Conway’s Life is in the more complex behaviors it can produce:
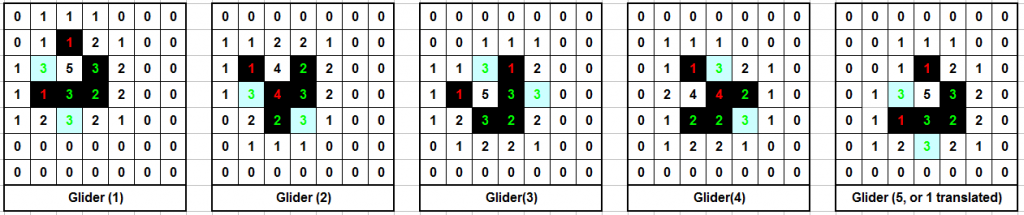
Shortly after it was invented, the “glider” was discovered — which can move diagonally. (There are four versions, each mirror images, which move in the four diagonal directions.)
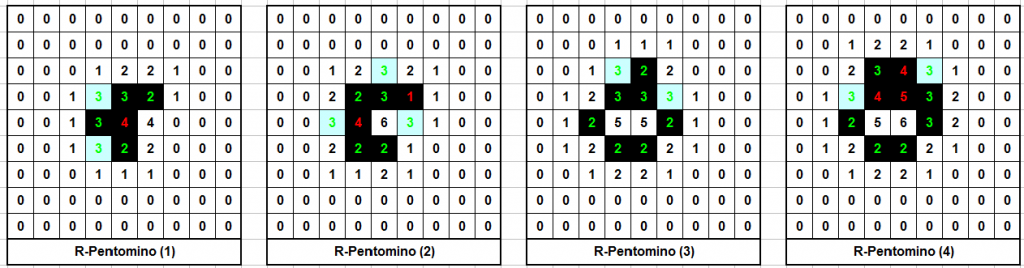
An excellent example of emergent complexity is the “R-Pentomino”: a set of five cells which explodes in a burst of activity, firing off several gliders until finally becoming stable over a thousand generations later(!)
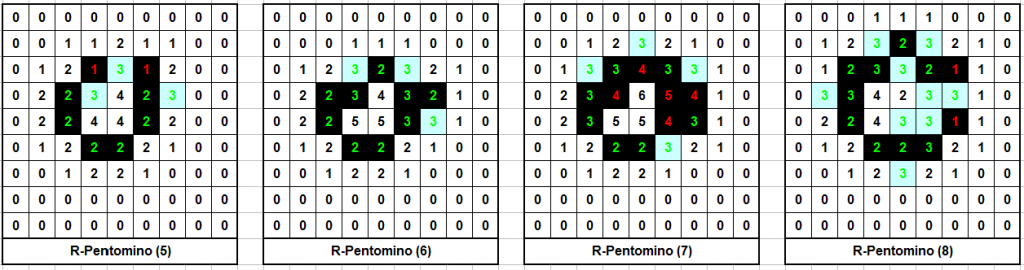
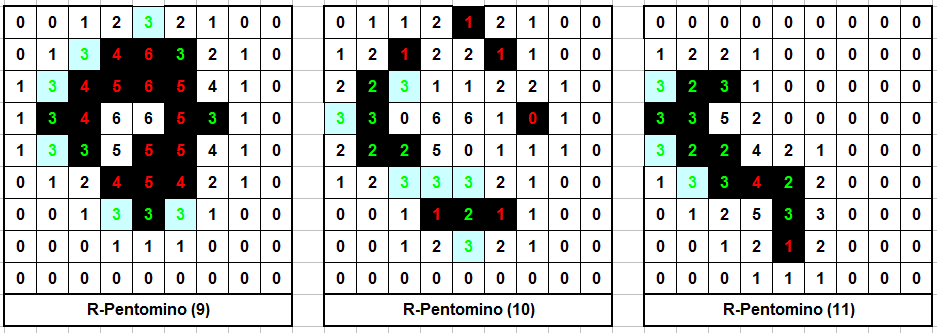
There are many more interesting examples out there. In fact, it has even been proven that Conway’s Life can be used to build a universal (Turing-complete) computer — albeit a very inefficient one. I recommend Life32 as a good, easy-to-use program to start your investigations into Life. If you’re interested in finding out more about some of the many fascinating Life constructs discovered, Stephen A. Silver has compiled an excellent Life Lexicon.