Minecraft!
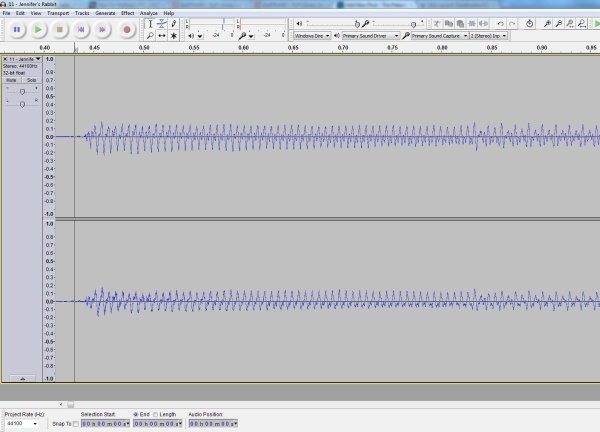
I’d heard about an interesting new world called “Minecraft,” so I thought I’d see what it was like. A short download later, an icon looking like a block of earth appeared on my desktop. Double-clicking it and filling in some information (Name the world? Okay. Random seed? Let’s go with 1024 for reproducibility. Graphics detail? Sock it to me. Do I want monsters? Naah — not just yet…), I found myself looking at a sunrise over a sandy tidal pool, with low hills on both sides.
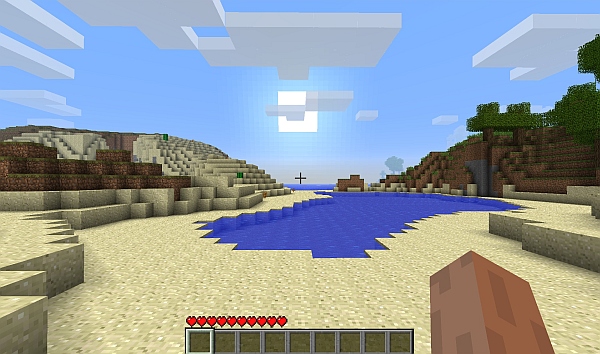
A new, blocky world awaits! (Click for larger.)
Something about this world was strange, though. It seemed that its creator followed the Integer Mythos. Think “Mario Brothers” (or “Donkey Kong,” for those of us old enough to have first associated Nintendo with Atari 2600 cartridges and coin-op arcade games.) In contrast to other worlds I’d visited, such as Cyrodiil, nearly everything in Minecraft is rendered in 1m x 1m x 1m blocks.
At first, this looks like a cheap way to avoid a lot of the work associated with creating a 3D virtual world. Make everything out of identical blocks, and lots of tasks become a lot easier. The gods must be lazy, I thought.
This kind of world has a definite appeal, though. Nearly all of the blocks in the world can be modified by digging and/or placing them. Various constructs can be made this way, from houses to mines to railroads and rudimentary roller coasters. The beauty of such an integer-based world is that it’s reproducible. A complex, intricate mechanism built in one location can be duplicated in another, given the same resources and space — and it will work exactly the same. One block of cobblestone (or dirt, or lava) is identical to any other block of the same type. Once you know how to build something, you can reproduce it elsewhere and be assured that it will work exactly the same way. (The framerates are excellent, too; glass-smooth throughout.)
There’s a lot to build, too. The world contains many kinds of raw materials, and there are many “recipes” for combining these to make different items. Some of the more useful ones are pickaxes, torches, shovels, axes, storage chests, etc. Get a block of wood from a tree and turn it into planks; take these planks and make a crafting table; use the larger surface of the crafting table to make a wood pickaxe; mine stone to make a stone pickaxe and a furnace; use the stone pickaxe to mine iron to melt in the furnace to make iron ore; use the iron ore to make an iron pickaxe… you get the point.
Even with the uniformity, though, there’s plenty of variety. There are over 100 kinds of blocks (so far); even in a modest 10x10x10 cube of blocks, there are more than 100^1000 possibilities. (That’s a one with 2,000 zeros after it.) And the world of Minecraft is much larger (much MUCH larger) than 10x10x10!
Eventually, I started to wonder — how big *was* this new world I found myself in? Would I eventually fill it up and run out of things to do? I climbed a nearby hill and looked around. The world seemed to end in fog some distance away. Not quite as big as Cyrodiil, then — I could walk over there without too much effort, I thought. I made a note of what the edge-of-the-map features looked like in one direction and started walking / swimming.
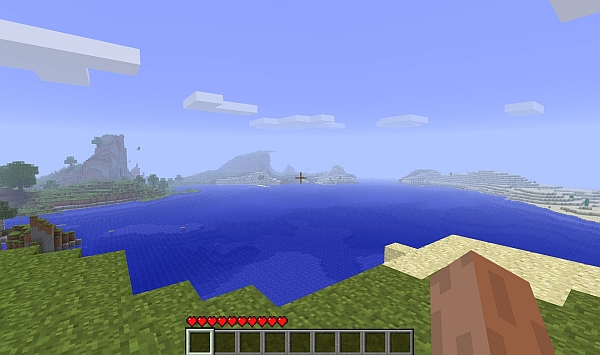
The view from a local hilltop. (Click for larger.)
Halfway there, I climbed another low hill to take a look. The features that were on the edge of the map were closer, with other features beyond them. This world was larger than it seemed; there was as much land ahead as I had seen before. Such a world was no doubt rendered by sections — and if these were programatically generated, the end of the world could be a long distance away, indeed. I turned back, deciding that there was a high probability that I wouldn’t be able to answer this question in-world anytime soon. (As it turned out, this was correct. Minecraft is very VERY big, and would take some 820 hours of constant walking to reach even the closest definition of the “end of the world.”)
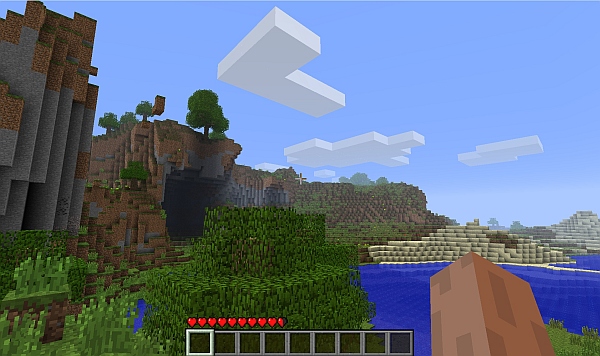
The view after traveling a bit. (Click for larger.)
I couldn’t find out how far the world extended in the cardinal directions — at least for now — but what about height and depth? Not knowing much about mining, but having had some luck moving dirt blocks around, I started building a tower. Blocks, as it turns out, can float in midair; physics works a bit differently here. This is unintuitive at first, but allows very minimalistic towers to be built: a 2×2 square of blocks, with one block per level in an ascending helix. (Just don’t fall more than a few meters!) A bit after reaching the clouds (58 levels up from where I started), the world topped out. Blocks could no longer be placed above this level. So there is a definite, reachable-but-reasonable limit to height.
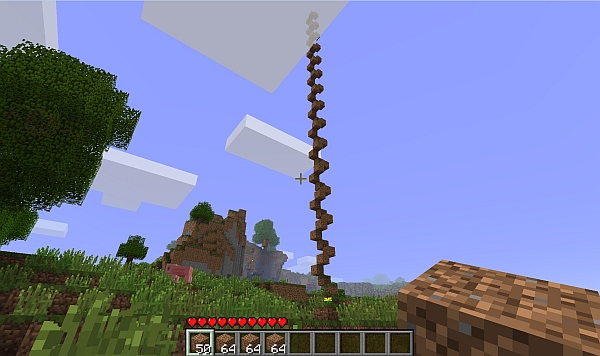
A helical stairway rising above the clouds. (Click for larger.)
What about depth? Along the same lines as the tower, I found that a 2×2 square could contain a spiral staircase down into the earth, lowering one meter for every 90 degrees turned. Whereas one block needed to be placed per level for the tower, three need to be excavated for a staircase in rock. (People in Minecraft are exactly two meters tall; the third block is needed for headroom when ascending and descending.)
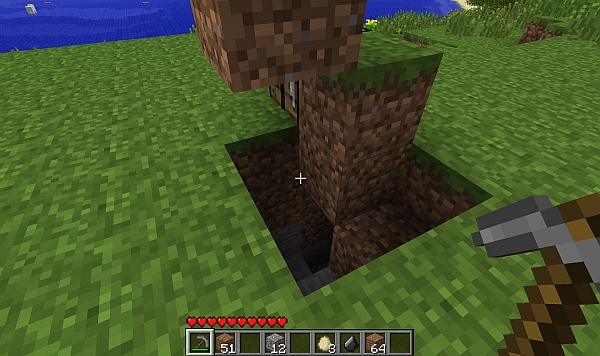
A 2x2 spiral stairway down into the earth. (Click for larger.)
After several meters, it got too dark to see, so I had to turn back (and learn how to make torches). Torches are formed from coal (or charcoal), plus a stick; you need to either mine charcoal using a pickaxe, or build a furnace and burn wood blocks. Once torches were available, I was able to continue my spiral staircase downwards for another 64 levels, eventually reaching impermeable bedrock (or “adminium” as it’s also called.) In places, reachable areas extended another four levels, making a total of 126 level changes — 127 levels — between the bottom and the top of the world. Add another level since avatars in Minecraft span two blocks, and you get 128 levels. A nice even number for computers, but not quite as nice and round as 256. Perhaps performance considerations limited the level span?
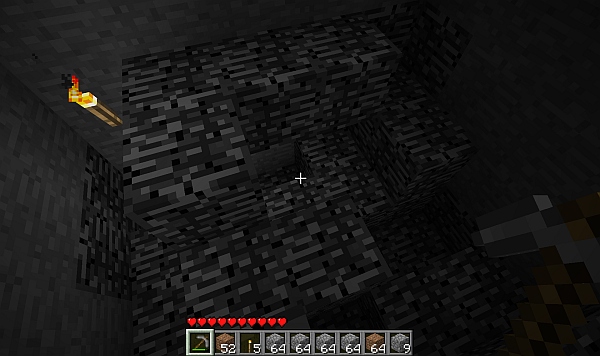
Impermeable bedrock at the bottom of the world. (Click for larger.)
Weight and volume are definitely more a state-of-mind thing than actual physical limitations. For instance, a Minecraft character can carry 36 items, including nine “equipped” slots, but not counting armor. Each of these “items” can be as many as 64 of a “stackable” object type, such as rock. This means that — even though each “stone block” represents a 1m x 1m x 1m block of stone, a Minecraft character (ostensibly human) can carry 2,304 of them without even really trying!
I decided it would be fun to show this graphically, so I loaded up my avatar with cobblestones and started building a 13x13x13 cube. This took 2,197 blocks, so I had 107 left over for decorations. Here is the result, with a 2x1x1 (avatar-sized) stack of dirt blocks in front of it, representing a Minecraft avatar.
- This is how much stone an avatar can carry at once. That cube is solid stone. (Click for larger.)
Technology exists in Minecraft, too — boats, railroads, gates, pistons, and even digital logic elements. It’s possible to build a working computer in Minecraft — but that’s a topic for another time.