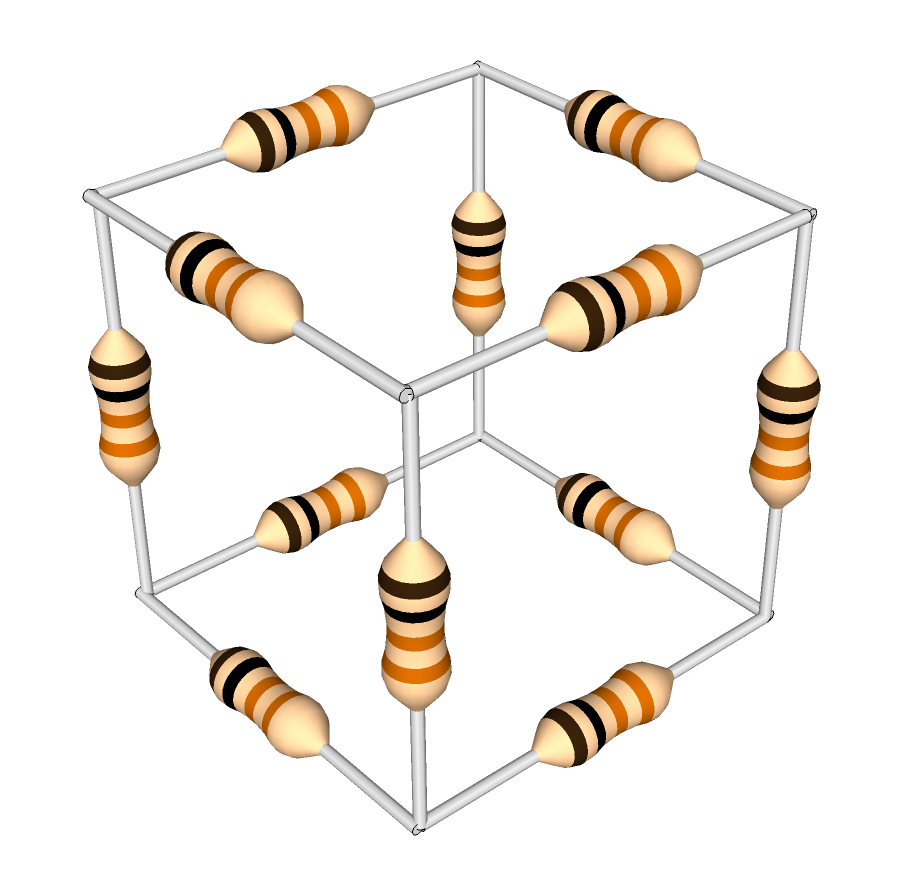
I came across an interesting puzzle a while ago (stated in one of the excellent Feynman Lectures on Physics): What is the resistance between two opposite corners of a cube made from 1-ohm resistors?
At first, the problem looks like it might just be an exercise in resistance simplification using the well-known laws of parallel and serial resistances: Serial resistances add linearly, and parallel resistances follow 1/R = 1/R1 + 1/R2 etc. Unfortunately, this one isn’t quite so simple — three resistors meet at each vertex of the cube, and no two are directly parallel to or in series with each other.
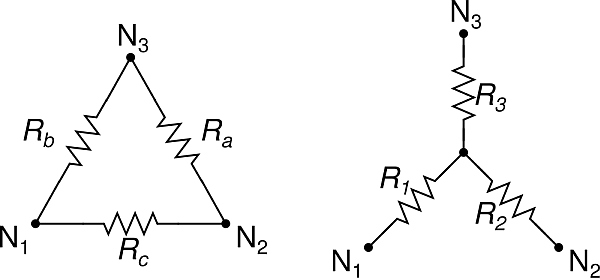
One solution to this problem is to use the Wye-Delta conversion formula. Each of the corners of the cube is the center node of three resistors in a wye configuration. These three resistors can be replaced, and the central node removed, by following the formula:
(formula from Wikipedia)
Rp in the formula is the sum of products — that is, R1R2 + R2R3 + R1R3.
(image from Wikipedia)
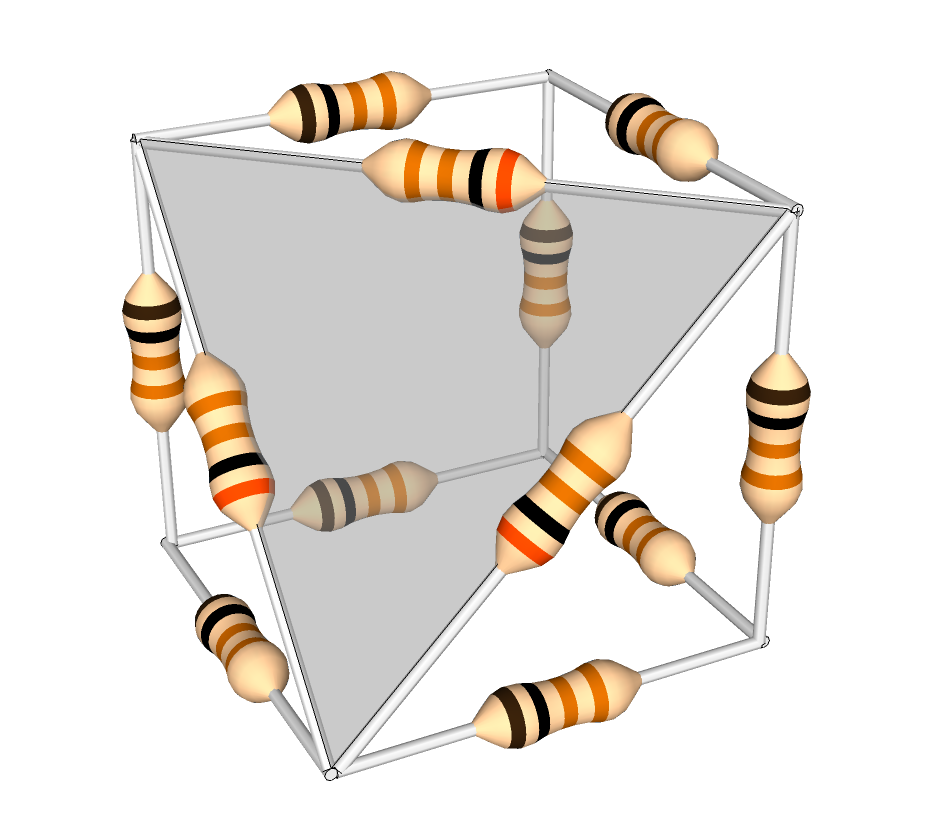
Using this formula, corners of the cube where three 1-ohm resistors meet can be removed; the three outer vertices of this wye are then connected by the equivalent network of one 3-ohm resistor between each pair of vertices (see image).
One way you can think about this is that, initially, the resistance between any two nodes of the wye is 2 ohms (the inbound resistor plus the outbound resistor.) In order for the delta network to be equivalent, this resistance must be the same; the value of the delta resistor connecting those two nodes, in parallel with the sum of the other two delta resistors (for the long path around the triangle), must equal the original value of the resistance between the two nodes of the wye. For a wye of 1-ohm resistors, this is 3 ohms, since a 3-ohm resistor in parallel with a 6-ohm equivalent will equal two ohms. (1/3 + 1/6 = 1/2)
You can continue reducing the network in this way — but it turns out that symmetry and a little common sense provide an easier way to solve the puzzle.
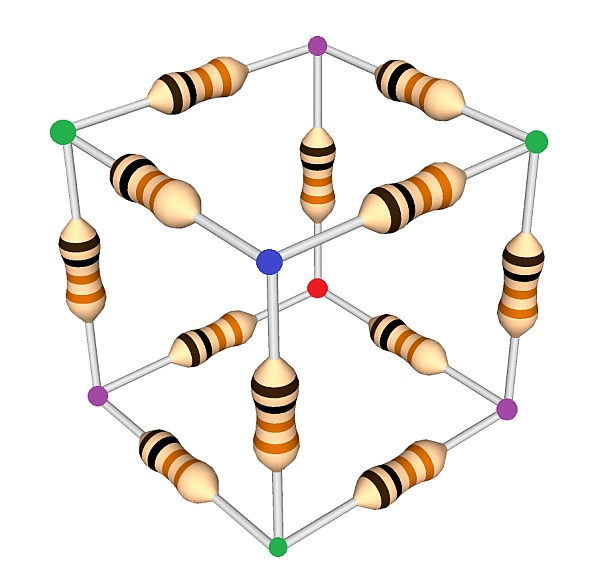
The cube, with equipotential points shown, assuming resistance measured between blue and red. (Click for larger.)
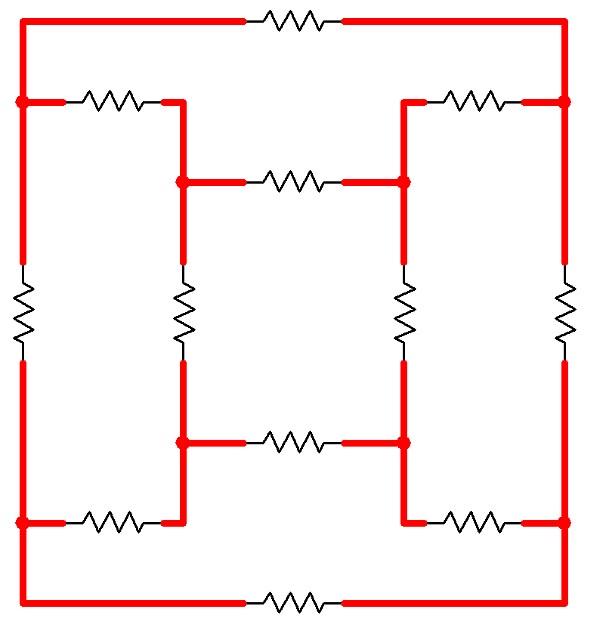
Suppose that in the cube above, a voltage source is connected between the blue and red nodes. The resulting current can be used to determine the overall resistance. To calculate this without resulting to Wye-Delta conversions, note that all of the “purple” nodes are at the same voltage (due to symmetry), and all of the “green” nodes are at the same voltage (also due to symmetry). Because of this, the three purple nodes and the three green nodes can therefore be connected by wires in order to simplify the analysis. Because no voltage difference exists between the nodes, no current will flow across these wires, so the nature of the circuit hasn’t been fundamentally changed.
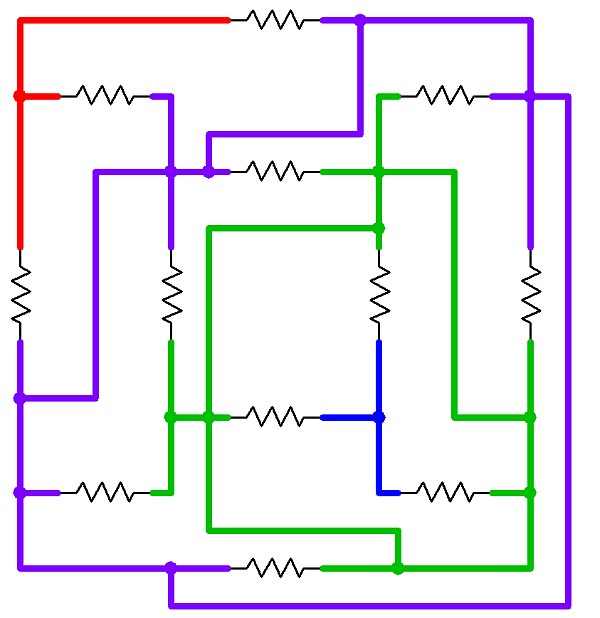
Here is a schematic of the original cube configuration…
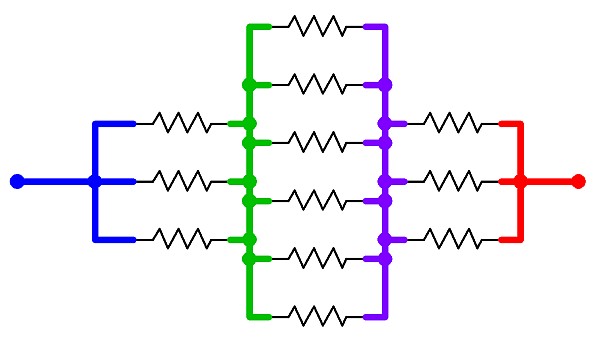
…and here is a schematic of the cube with the equipotential connections in place.
The problem now becomes trivially easy. The blue node is connected to the green node via three 1-ohm resistors; the green node is connected to the purple node via six 1-ohm resistors; and the purple node is connected to the red node via another three 1-ohm resistors.
The total circuit resistance is therefore 1/3 + 1/6 + 1/3 ohms, or 5/6 ohm.